Pular para o conteúdo principal

Regressão Linear Simples

Visual​

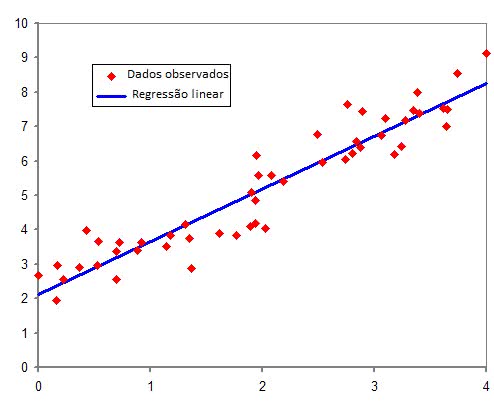
Representação de uma regressão linear. O eixo x apresenta os números 0, 1, 2, 3 e 4. O eixo y apresenta os números de 0 até 10. A reta é crescente e corta o eixo y no ponto y=2. Existem diversos pontos marcados em torno da reta, espalhados com alguma aleatóriedade.

Fórmula​

y=β0+β1xy = \beta_0 + \beta_1 x

O objetivo é calcular β0\beta_0 e β1\beta_1.

Coeficientes

β0\beta_0 é chamado de intercepto (coeficiente linear da reta). β1\beta_1 é chamado de inclinação (coeficiente angular da reta).reta.

Variáveis
  • A variável yy é chamada de variável dependente, ou resposta.
  • A variável xx é chamda de variável independente ou explicativa.

Determinação dos Parâmetros​

Inclinação​

β1=∑xiyi−(∑xi)⋅(∑yi)n∑xi2−(∑xi)2n\beta_1 = \dfrac{ \displaystyle\sum x_i y_i - \dfrac{ \big( \displaystyle\sum x_i \big) \cdot \big( \displaystyle\sum y_i \big) }{n} }{ \displaystyle\sum x_i^2 - \dfrac{ \big( \sum x_i \big)^2 }{n} }

Intercepto​

β0=yˉ−β1xˉ\beta_0 = \bar{y} - \beta_1\bar{x}